The Forces in (Figure 1) Act on a 10 Kg Object You May Want to Review (Pages 135 - 137)

Muscles, basic, and joints are some of the near interesting applications of statics. There are some surprises. Muscles, for case, exert far greater forces than we might think. Figure 1 shows a forearm belongings a book and a schematic diagram of an coordinating lever system. The schematic is a proficient approximation for the forearm, which looks more complicated than it is, and we tin can get some insight into the way typical muscle systems function past analyzing it.

Muscles can only contract, so they occur in pairs. In the arm, the biceps muscle is a flexor—that is, it closes the limb. The triceps muscle is an extensor that opens the limb. This configuration is typical of skeletal muscles, basic, and joints in humans and other vertebrates. Most skeletal muscles exert much larger forces within the body than the limbs employ to the exterior world. The reason is clear one time nosotros realize that most muscles are fastened to bones via tendons close to joints, causing these systems to have mechanical advantages much less than one. Viewing them as simple machines, the input force is much greater than the output force, as seen in Figure i.

Effigy one. (a) The effigy shows the forearm of a person holding a book. The biceps exert a force F_B to support the weight of the forearm and the volume. The triceps are causeless to be relaxed. (b) Hither, you can view an approximately equivalent mechanical system with the pivot at the elbow joint as seen in Example 1.

Example 1. Muscles Exert Bigger Forces Than Yous Might Think

Calculate the force the biceps muscle must exert to hold the forearm and its load equally shown in Figure ane, and compare this forcefulness with the weight of the forearm plus its load. You may accept the information in the figure to be accurate to iii significant figures.

Strategy

There are four forces interim on the forearm and its load (the system of interest). The magnitude of the forcefulness of the biceps is F _B; that of the elbow joint is F _E; that of the weights of the forearm is w _a, and its load is westward _b. Ii of these are unknown (F _B and F _E), then that the first condition for equilibrium cannot by itself yield F _B. But if we use the 2d status and cull the pin to exist at the elbow, and then the torque due to F _{Due east} is zero, and the only unknown becomes F _B.

Solution

The torques created past the weights are clockwise relative to the pivot, while the torque created past the biceps is counterclockwise; thus, the second condition for equilibrium (internet τ = 0) becomes

r ₂ west _a+r _iii w _b=r ₁ F _B

Notation that sin θ = ane for all forces, since θ= 90º for all forces. This equation can easily be solved for F _B in terms of known quantities, yielding

[latex]{F}_{\text{B}}=\frac{{r}_{2}{due west}_{\text{a}}+{r}_{3}{due west}_{\text{b}}}{{r}_{1}}\\[/latex].

Entering the known values gives

[latex]{F}_{\text{B}}=\frac{\left(0\text{.}\text{160}\text{m}\right)\left(2\text{.}\text{50}\text{kg}\right)\left(9\text{.}\text{80}{\text{chiliad/due south}}^{2}\right)+\left(0\text{.}\text{380}\text{m}\correct)\left(4\text{.}\text{00}\text{kg}\right)\left(9\text{.}\text{80}{\text{m/south}}^{two}\correct)}{0\text{.}\text{0400}\text{ m}}\\[/latex]

which yields

F _B= 470 N.

Now, the combined weight of the arm and its load is (6.l kg)(9.80 grand/southⁱⁱ) = 63.7 N, so that the ratio of the strength exerted by the biceps to the full weight is

[latex]\frac{{F}_{\text{B}}}{{w}_{\text{a}}+{west}_{\text{b}}}=\frac{\text{470}}{\text{63}\text{.}seven}=seven\text{.}\text{38}\\[/latex].

Give-and-take

This means that the biceps muscle is exerting a force 7.38 times the weight supported.

In the in a higher place example of the biceps musculus, the bending between the forearm and upper arm is 90°. If this angle changes, the forcefulness exerted by the biceps musculus also changes. In improver, the length of the biceps muscle changes. The force the biceps muscle tin can exert depends upon its length; information technology is smaller when it is shorter than when it is stretched.

Very large forces are also created in the joints. In the previous example, the downward force F _E exerted past the humerus at the elbow joint equals 407 Northward, or 6.38 times the total weight supported. (The calculation of F _Eastward is straightforward and is left as an end-of-affiliate trouble.) Because muscles can contract, but not expand beyond their resting length, joints and muscles often exert forces that act in opposite directions and thus subtract. (In the in a higher place example, the upward force of the musculus minus the downward strength of the joint equals the weight supported—that is, 470 Northward–407 N = 63 North, approximately equal to the weight supported.) Forces in muscles and joints are largest when their load is a long distance from the articulation, as the book is in the previous example.

In racquet sports such as tennis the constant extension of the arm during game play creates large forces in this style. The mass times the lever arm of a tennis racquet is an important gene, and many players use the heaviest racquet they can handle. It is no wonder that joint deterioration and damage to the tendons in the elbow, such as "tennis elbow," can event from repetitive motion, undue torques, and possibly poor racquet selection in such sports. Various tried techniques for holding and using a racquet or bat or stick not only increases sporting prowess but can minimize fatigue and long-term damage to the body. For example, lawn tennis balls correctly hit at the "sweet spot" on the racquet volition result in little vibration or touch force beingness felt in the racquet and the body—less torque as explained in Collisions of Extended Bodies in Two Dimensions. Twisting the manus to provide top spin on the ball or using an extended rigid elbow in a backhand stroke tin also beal the tendons in the elbow.

Grooming coaches and physical therapists use the knowledge of relationships between forces and torques in the handling of muscles and joints. In physical therapy, an practice routine tin can utilise a particular force and torque which can, over a period of time, revive muscles and joints. Some exercises are designed to be carried out nether water, because this requires greater forces to be exerted, farther strengthening muscles. However, connecting tissues in the limbs, such as tendons and cartilage besides as joints are sometimes damaged by the big forces they conduct. Often, this is due to accidents, just heavily muscled athletes, such as weightlifters, tin can tear muscles and connecting tissue through effort alone.

The back is considerably more complicated than the arm or leg, with various muscles and joints betwixt vertebrae, all having mechanical advantages less than ane. Dorsum muscles must, therefore, exert very large forces, which are borne by the spinal cavalcade. Discs crushed by mere exertion are very common. The jaw is somewhat exceptional—the masseter muscles that close the jaw have a mechanical advantage greater than ane for the back teeth, allowing us to exert very large forces with them. A cause of stress headaches is persistent clenching of teeth where the sustained large forcefulness translates into fatigue in muscles effectually the skull.

Effigy 2 shows how bad posture causes back strain. In part (a), we see a person with adept posture. Note that her upper trunk's cg is directly to a higher place the pivot point in the hips, which in turn is directly above the base of back up at her anxiety. Because of this, her upper trunk'southward weight exerts no torque near the hips. The simply force needed is a vertical force at the hips equal to the weight supported. No muscle action is required, since the bones are rigid and transmit this strength from the floor. This is a position of unstable equilibrium, merely only small forces are needed to bring the upper body back to vertical if it is slightly displaced. Bad posture is shown in part (b); nosotros see that the upper trunk'due south cg is in front of the pin in the hips. This creates a clockwise torque around the hips that is counteracted by muscles in the lower back. These muscles must exert large forces, since they have typically small mechanical advantages. (In other words, the perpendicular lever arm for the muscles is much smaller than for the cg.) Poor posture can also cause muscle strain for people sitting at their desks using computers. Special chairs are available that allow the body's CG to be more easily situated above the seat, to reduce back pain. Prolonged muscle action produces muscle strain. Note that the cg of the entire trunk is still straight above the base of support in function (b) of Figure 2. This is compulsory; otherwise the person would not be in equilibrium. We lean forwards for the same reason when carrying a load on our backs, to the side when carrying a load in one arm, and backward when conveying a load in front of u.s.a., as seen in Figure 3.

Figure 2. (a) good posture places the upper body'due south cg over the pivots in the hips, eliminating the need for muscle action to balance the body. (b) Poor posture requires exertion by the back muscles to annul the clockwise torque produced effectually the pivot by the upper body's weight. The back muscles have a modest effective perpendicular lever arm, r _b⊥, and must therefore exert a large force F _b. Note that the legs lean astern to keep the cg of the entire trunk above the base of operations of back up in the anxiety.

You have probably been warned confronting lifting objects with your back. This action, even more than bad posture, can cause muscle strain and damage discs and vertebrae, since abnormally big forces are created in the back muscles and spine.

Effigy 3. People adjust their stance to maintain balance. (a) A begetter carrying his son piggyback leans forward to position their overall cg above the base of support at his feet. (b) A student conveying a shoulder bag leans to the side to continue the overall cg over his feet. (c) Another pupil carrying a load of books in her arms leans backward for the same reason.

Example 2. Do Not Elevator with Your Back

Consider the person lifting a heavy box with his dorsum, shown in Figure 4. (a) Calculate the magnitude of the force F _B– in the dorsum muscles that is needed to support the upper body plus the box and compare this with his weight. The mass of the upper body is 55.0 kg and the mass of the box is 30.0 kg. (b) Calculate the magnitude and management of the forcefulness F ₅– exerted by the vertebrae on the spine at the indicated pivot point. Again, data in the effigy may be taken to be accurate to three meaning figures.

Strategy

By now, we sense that the second condition for equilibrium is a skilful place to showtime, and inspection of the known values confirms that it can be used to solve for F _B– if the pivot is chosen to exist at the hips. The torques created past w _ub and westward _box– are clockwise, while that created past F _B– is counterclockwise.

Solution for (a)

Using the perpendicular lever arms given in the figure, the second condition for equilibrium (cyberspaceτ = 0) becomes

(0.350 g)(55.0 kg)(9.80 1000/south²) + (0.500 m)(30.0 kg)(9.lxxx one thousand/sⁱⁱ) = (0.0800 m)F _B.

Solving for F _B yields

F _B= iv.20 × ten³ N.

The ratio of the forcefulness the back muscles exert to the weight of the upper trunk plus its load is

[latex]\frac{{F}_{\text{B}}}{{west}_{\text{ub}}+{west}_{\text{box}}}=\frac{\text{4200 N}}{\text{833 N}}=\text{5.04}\\[/latex].

This force is considerably larger than it would exist if the load were non present.

Solution for (b)

More important in terms of its damage potential is the force on the vertebrae F _V. The first condition for equilibrium (net F = 0) can exist used to find its magnitude and direction. Using y for vertical and ten for horizontal, the condition for the net external forces along those axes to be zero

net F_y  = 0 and F_x = 0

Starting with the vertical ( y ) components, this yields

[latex]{F}_{\text{V}y}-{w}_{\text{ub}}-{w}_{\text{box}}-{F}_{\text{B}}\sin{29.0}^{\circ}=0\\[/latex]

Thus,

[latex]\begin{array}{lll}{F}_{\text{5}y}& =& {due west}_{\text{ub}}+{westward}_{\text{box}}+{F}_{\text{B}}\sin{29.0}^{\circ}\ & =& \text{833 Northward}+\left(\text{4200 N}\right)\sin{29.0}^{\circ}\end{array}\\[/latex]

yielding

F _Vy = 2.87 × 10³ N.

Similarly, for the horizontal ( 10 ) components,

[latex]{F}_{\text{5}ten}-{F}_{\text{B}}\cos{29.0}^{\circ}=0\\[/latex]

yielding

F _Vx = three.67 × 10^three N.

The magnitude of F₅ is given past the Pythagorean theorem:

[latex]{{F}_{\text{5}}}=\sqrt{{{F}_{\text{5}x}}^{two}+{{F}_{\text{5}y}}^{2}}=\text{4.66}\times {10}^{three}\text{ Due north}\\[/latex].

The direction of F_V is

[latex]\theta =\tan^{-one}\left(\frac{{F}_{\text{Five}y}}{{F}_{\text{V}x}}\right)=38.0^{\circ}\\[/latex].

Note that the ratio of F _V to the weight supported is

[latex]\frac{{F}_{\text{V}}}{{w}_{\text{ub}}+{west}_{\text{box}}}=\frac{\text{4660 N}}{\text{833 Due north}}=5.59\\[/latex].

Word

This force is almost v.6 times greater than it would be if the person were standing erect. The trouble with the back is non and so much that the forces are big—because similar forces are created in our hips, knees, and ankles—merely that our spines are relatively weak. Proper lifting, performed with the back cock and using the legs to enhance the body and load, creates much smaller forces in the back—in this case, well-nigh 5.6 times smaller.

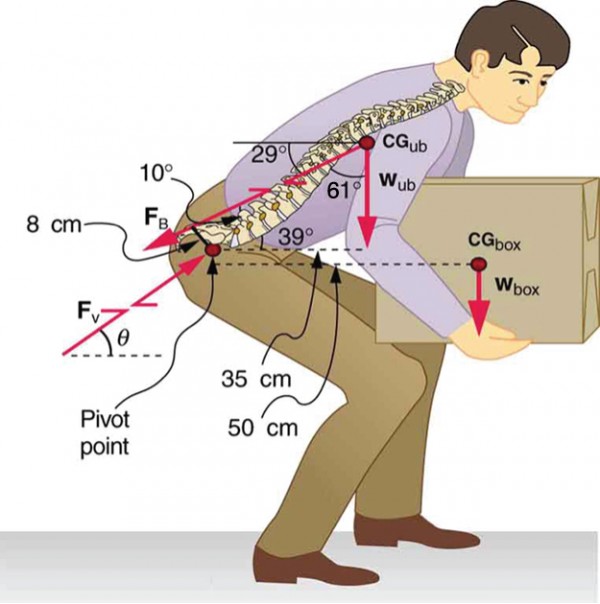
Figure 4. This figure shows that large forces are exerted by the back muscles and experienced in the vertebrae when a person lifts with their back, since these muscles take small constructive perpendicular lever artillery. The data shown hither are analyzed in the preceding example, Example 2.

What are the benefits of having most skeletal muscles fastened so shut to joints? 1 advantage is speed considering small-scale muscle contractions can produce big movements of limbs in a short flow of fourth dimension. Other advantages are flexibility and agility, fabricated possible past the big numbers of joints and the ranges over which they function. For instance, it is difficult to imagine a arrangement with biceps muscles attached at the wrist that would exist capable of the wide range of movement we vertebrates possess.

There are some interesting complexities in existent systems of muscles, bones, and joints. For instance, the pivot point in many joints changes location as the joint is flexed, and so that the perpendicular lever artillery and the mechanical advantage of the system change, too. Thus the strength the biceps muscle must exert to concord up a book varies as the forearm is flexed. Similar mechanisms operate in the legs, which explain, for example, why there is less leg strain when a cycle seat is fix at the proper tiptop. The methods employed in this section give a reasonable description of real systems provided enough is known virtually the dimensions of the system. There are many other interesting examples of force and torque in the body—a few of these are the subject of end-of-affiliate problems.

Section Summary

• Statics plays an of import part in understanding everyday strains in our muscles and bones.
• Many lever systems in the trunk have a mechanical advantage of significantly less than one, as many of our muscles are attached shut to joints.
• Someone with good posture stands or sits in such as way that their heart of gravity lies direct in a higher place the pin indicate in their hips, thereby avoiding back strain and damage to disks.

Conceptual Questions

i. Why are the forces exerted on the outside world by the limbs of our bodies normally much smaller than the forces exerted past muscles inside the body?

ii. Explicate why the forces in our joints are several times larger than the forces we exert on the outside globe with our limbs. Can these forces exist fifty-fifty greater than muscle forces?

3. Certain types of dinosaurs were bipedal (walked on 2 legs). What is a proficient reason that these creatures invariably had long tails if they had long necks?

iv. Swimmers and athletes during competition demand to become through certain postures at the beginning of the race. Consider the balance of the person and why start-offs are so of import for races.

five. If the maximum force the biceps musculus tin can exert is k N, tin we option upwardly an object that weighs 1000 N? Explain your answer.

half dozen. Suppose the biceps muscle was attached through tendons to the upper arm shut to the elbow and the forearm near the wrist. What would be the advantages and disadvantages of this blazon of construction for the motility of the arm?

seven. Explain one of the reasons why pregnant women often suffer from back strain late in their pregnancy.

Exercises

1. Verify that the force in the elbow joint in Example 1: Muscles Exert Bigger Forces Than Yous Might Recall (above) is 407 N, as stated in the text.

ii. 2 muscles in the back of the leg pull on the Achilles tendon as shown in Effigy 5. What full forcefulness do they exert?

Figure v. The Achilles tendon of the posterior leg serves to attach plantaris, gastrocnemius, and soleus muscles to calcaneus bone.

3. The upper leg muscle (quadriceps) exerts a forcefulness of 1250 North, which is carried by a tendon over the kneecap (the patella) at the angles shown in Figure vi. Find the direction and magnitude of the force exerted by the kneecap on the upper leg bone (the femur).

Effigy 6. The articulatio genus works like a hinge to bend and straighten the lower leg. It permits a person to sit, stand, and pivot.

iv. A device for exercising the upper leg muscle is shown in Figure 7, together with a schematic representation of an equivalent lever organisation. Calculate the force exerted by the upper leg musculus to elevator the mass at a constant speed. Explicitly show how yous follow the steps in the Trouble-Solving Strategy for static equilibrium in Applications of Statistics, Including Problem-Solving Strategies.

Effigy 7. A mass is connected by pulleys and wires to the ankle in this exercise device.

5. A person working at a drafting board may hold her head equally shown in Figure 8, requiring muscle action to support the head. The 3 major acting forces are shown. Calculate the direction and magnitude of the forcefulness supplied by the upper vertebrae F ₅ to hold the head stationary, assuming that this strength acts along a line through the center of mass as do the weight and musculus force.

Effigy 8.

6. We analyzed the biceps muscle example with the angle between forearm and upper arm prepare at 90º. Using the same numbers as in Example one: Muscles Exert Bigger Forces Than You lot Might Call up(above), find the force exerted by the biceps musculus when the bending is 120º and the forearm is in a downwardly position.

seven. Fifty-fifty when the head is held cock, as in Figure nine, its center of mass is not directly over the principal point of support (the atlanto-occipital joint). The muscles at the back of the neck should therefore exert a force to proceed the head erect. That is why your head falls frontwards when yous fall asleep in the class. (a) Calculate the force exerted past these muscles using the information in the figure. (b) What is the force exerted by the pivot on the head?

Figure nine. The middle of mass of the caput lies in front end of its major point of support, requiring musculus action to hold the head erect. A simplified lever system is shown.

eight. A 75-kg human being stands on his toes by exerting an upward force through the Achilles tendon, as in Figure ten. (a) What is the force in the Achilles tendon if he stands on one foot? (b) Summate the force at the pin of the simplified lever organisation shown—that force is representative of forces in the ankle joint.

Figure 10.

9. A father lifts his child as shown in Figure eleven. What force should the upper leg muscle exert to lift the child at a abiding speed?

Figure 11. A kid being lifted by a male parent'due south lower leg.

10. Different nigh of the other muscles in our bodies, the masseter muscle in the jaw, as illustrated in Figure 12, is attached relatively far from the joint, enabling large forces to be exerted by the dorsum teeth. (a) Using the information in the figure, summate the force exerted by the lower teeth on the bullet. (b) Calculate the forcefulness on the joint.

Effigy 12. A person clenching a bullet between his teeth.

11. Integrated ConceptsSuppose we supercede the 4.0-kg book in Exercise 7 of the biceps muscle with an elastic exercise rope that obeys Hooke'due south Police. Presume its force constant k = 600 N/one thousand (a) How much is the rope stretched (past equilibrium) to provide the aforementioned force F _B equally in this case? Assume the rope is held in the paw at the same location as the book. (b) What forcefulness is on the biceps muscle if the exercise rope is pulled straight upwards so that the forearm makes an angle of 25º with the horizontal? Presume the biceps muscle is still perpendicular to the forearm.

12. (a) What force should the woman in Figure 13 exert on the flooring with each hand to do a push-up? Assume that she moves upward at a constant speed. (b) The triceps muscle at the back of her upper arm has an effective lever arm of 1.75 cm, and she exerts force on the floor at a horizontal distance of 20.0 cm from the elbow joint. Summate the magnitude of the force in each triceps muscle, and compare it to her weight. (c) How much piece of work does she do if her center of mass rises 0.240 m? (d) What is her useful power output if she does 25 pushups in one minute?

Effigy 13.

13. You have but planted a sturdy ii-m-tall palm tree in your front backyard for your mother's birthday. Your brother kicks a 500 g ball, which hits the top of the tree at a speed of five m/s and stays in contact with information technology for ten ms. The brawl falls to the ground near the base of the tree and the recoil of the tree is minimal. (a) What is the forcefulness on the tree? (b) The length of the sturdy section of the root is only 20 cm. Furthermore, the soil around the roots is loose and we tin can presume that an effective force is applied at the tip of the 20 cm length. What is the effective force exerted by the cease of the tip of the root to continue the tree from toppling? Presume the tree volition exist uprooted rather than curve. (c) What could yous accept washed to ensure that the tree does not uproot easily?

14. Unreasonable ResultsSuppose two children are using a compatible seesaw that is 3.00 m long and has its center of mass over the pivot. The first child has a mass of 30.0 kg and sits 1.xl m from the pin. (a) Calculate where the second xviii.0 kg child must sit to residual the seesaw. (b) What is unreasonable nigh the result? (c) Which premise is unreasonable, or which premises are inconsistent?

15. Construct Your Own ProblemConsider a method for measuring the mass of a person's arm in anatomical studies. The subject lies on her dorsum, extends her relaxed arm to the side and two scales are placed below the arm. One is placed nether the elbow and the other nether the back of her hand. Construct a problem in which you summate the mass of the arm and find its middle of mass based on the scale readings and the distances of the scales from the shoulder articulation. You must include a gratuitous body diagram of the arm to directly the analysis. Consider changing the position of the scale under the hand to provide more than information, if needed. You may wish to consult references to obtain reasonable mass values.

Selected Solutions to Problems & Exercises

one. [latex]\begin{array}{lll}{F}_{\text{B}}&=&\text{470 N; }{r}_{one}=\text{four.00 cm; }{w}_{\text{a}}=\text{2.fifty kg; }{r}_{2}=\text{xvi.0 cm; }{w}_{\text{b}}=\text{4.00 kg; }{r}_{3}=\text{38.0 cm}\\ {F}_{\text{E}}& =& {westward}_{\text{a}}\left(\frac{{r}_{ii}}{{r}_{1}}-1\right)+{w}_{\text{b}}\left(\frac{{r}_{iii}}{{r}_{ane}}-1\right)\\ & =& \left(\text{ii.fifty kg}\right)\left(9.80\text{m}/{\text{s}}^{two}\right)\left(\frac{\text{sixteen.0 cm}}{\text{4.0 cm}}-1\right)\\ & & +\left(\text{4.00 kg}\right)\left(9.eighty\text{m}/{\text{s}}^{2}\right)\left(\frac{\text{38.0 cm}}{\text{4.00 cm}}-1\correct)\\ & =& \text{407 Due north}\cease{array}\\[/latex]

3. 1.one ten ten³ N, θ = 190 º ccw from positive 10– axis

5. F ₅ = 97 North, θ = 59º

vii. (a) 25 North downwards (b) 75 N up

9. (a) F _A = 2.21 × 10³ North upward (b) F _B = 2.94 × 10³ Due north  downward

11. (a)F _{teeth on bullet} = 1.2 × tenⁱⁱ N upward (b) F _J = 84 N downward

13. (a) 147 N downward (b) 1680 N, 3.4 times her weight (c) 118 J (d) 49.0 W

fifteen.  (a) [latex]{\bar{ten}}_{2}=\text{ii.33 thousand}\\[/latex] (b) The seesaw is 3.0 k long, and hence, there is only i.50 thousand of board on the other side of the pivot. The 2d child is off the lath. (c) The position of the first child must exist shortened, i.eastward. brought closer to the pivot.

robinsonabouty.blogspot.com

Source: https://courses.lumenlearning.com/physics/chapter/9-6-forces-and-torques-in-muscles-and-joints/

Share this post